超声波在悬浮液中的衰减
发布日期:2015-06-09 08:42 浏览次数:次
苏杭丽
(南京财经大学信息工程学院,江苏南京 210003)
摘要: 通过研究悬浮液对超声波振幅的衰减问题,指出Lamb 衰减理论在工程应用中存在2 个问题:(a)在粗粒区,Lamb 理论的衰减系数与试验数据有较大差异;(b)Lamb 理论认为声密度与颗粒体积分数呈线性关系,与试验结果不符。针对Lamb 理论存在的问题,对Lamb 理论中的散射衰减项、声密度与颗粒体积分数的关系进行了修正。结果表明,修正后的理论能更好地拟合试验曲线。
关键词: 超声波;悬浮液;超声波振幅衰减系数;声密度;有效粒子数
中图分类号:TB52+9 文献标志码:A 文章编号:1000 1980(2012)06 0710 05
当一束平行超声波通过厚度为x 的悬浮液时,由指数衰减定律得
I = I0e-ax (1)
式中:I0,I———入射、出射超声波的强度;a———超声波振幅衰减系数。
有关衰减系数的研究很多[1-7] ,1948 年Lamb 等[7] 提出了一个比较实用的公式:
式中:k———波数;cv———颗粒的体积分数;r———悬浮液中颗粒的半径;c1———悬浮液中颗粒的密度;c0———媒
质密度;λ———超声波波长;f———超声波频率;μ———黏滞系数。
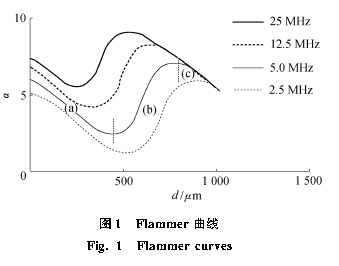
由式(2)可以看出, a 是颗粒粒径(d =2r)的复杂函数。式(2)中括号中的第1 项是由散射造成的衰减,类似光学中的瑞利散射,为d 的单调递增函数;中括号中的第2 项为黏滞衰减项,是d 的单调递减函数。但是,1963 年Flammer[8] 给出cv 为0. 1% 时不同频率超声波束所对应的a 与d 的关系曲线(图1)。从图1 可以看出,不同频率超声波束的a 与d 关系曲线近乎平行。因此,式(2)不能很好地对图1 中的曲线进行模拟。
将式(1)和式(2)进行整理得
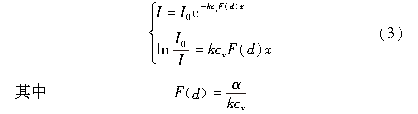
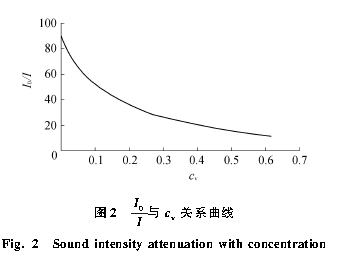
由式(3)可得:超声波强度I 随cv 呈指数衰减;定义Y =ln*I0/I为声密度,则Y 与cv 为线性正相关。而文献[9]给出的Y 与cv 关系曲线不完全符合式(3)所描述的Y 与cv 成正比的关系(图2)。
为解决理论公式(2)(3)不能很好地模拟试验曲线的问题,笔者对Lamb 公式中的散射衰减项及Y 与cv 的线性关系进行修正,使2 个理论公式能够较好地对图1、图2中的试验曲线进行模拟。
1 散射衰减项的修正
式(2)中括号中的第1 项可以用来说明图1 曲线上的(b)段。式(2)中括号中的第2 项可以用来说明图1 中的(a)段曲线。因此,式(2)只说明a 存在一个极小值,但是图1 显示a 除了存在一个极小值外,还存在一个极大值以及(c)段曲线。文献[10]指出式(2)不适用(c)段曲线,因此,可以认为Lamb 公式中黏滞衰减项不需要修正。因为瑞利散射只适用于微细粒子而无法模拟粗粒子的散射,因此式(2)中的瑞利散射项需要修正。修正的前提是:粗粒子对超声波的散射类似于对光波的散射,即对于超声波的散射,颗粒只是相移元件;超声波经过颗粒会产生相位角为c 的相移,产生相移的超声波与那些没有相移的超声波束发生干涉形成散射,其散射系数K 可用Hulst 模型[11] 求出:
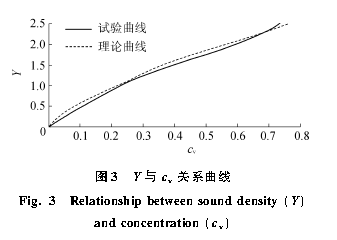
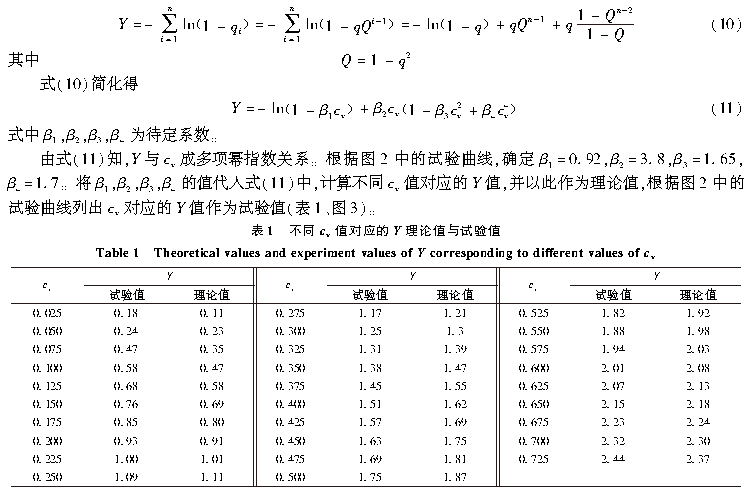
式(7)等号右边的第1 项为黏滞衰减项,即为图1 中曲线的(a)段;等号右边第2 项为修正的Hulst 散射项。根据文献[13],Hulst 散射曲线随d 增大而增大,K 首先以瑞利模型方式增加并达到极大值,然后逐渐随d 增加而减小,形成1 个单峰。当d 很大时,式(7)等号右边的第2 项约为cv 3d 。因此,式(7)能全面解释图1 中曲线的(a)段、(b)段和(c)段。2 Y 与cv 线性关系的修正式(3)说明Y 和cv 成正比关系。图3 是由图2 改绘而成的Y ~ cv 曲线。由图3 可知,Y 与cv 的关系线不是一条简单的直线,而是一条中间扭曲的S 形曲线。
2. 1 线性消声模型
平行超声波束照射悬浮液,经水层颗粒吸收散射以后,超声波束被衰减,如图4(a)所示[14] 。设悬浮液的厚度为L,分为n 层,每层厚度为h,S 为水槽面积。则单位截面积上每层颗粒数为Nh;h 距离内,单位截面的消声系数为
线性消声模型中每个水层的消声作用相互独立,因此,每层的消声系数q 相等。
式(9)即为指数衰减定律式(1),其只适用于q 比较低的情况。即只有当颗粒体积分数很低时,每一水层颗粒的消声作用才相互独立。
2. 2 非线性消声模型
随着颗粒体积分数增加,前各层的颗粒对后层颗粒的消声作用有遮蔽作用,使后面各层颗粒接受声波束作用的机会少于前面各层[13] ,所以各层的有效消声颗粒数不同。如果只考虑2 次重叠作用,ni 为第i 层的有效粒子数,qi 为第i 层的消声系数(图4(b)),则Y 的表达式为
从图3 可以看出,Y 的理论值曲线与试验曲线的变化趋势基本一致,即一次导数、二次导数和极限值都基本一致,表明修正后Y 的理论公式能较好地模拟试验曲线。
3 结 语
对Lamb 公式中的散射衰减项进行修正,修正后的lamb 公式能更好地模拟试验曲线。粒子对声波的散射类似于对光波的散射。提出了有效粒子数的概念,通过对Y 与cv 关系式进行修正,得出Y 是cv 的多项指数函数,且此函数能较好地拟合试验曲线的结论。
(责任编辑:admin)
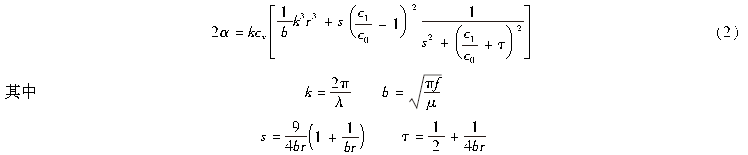
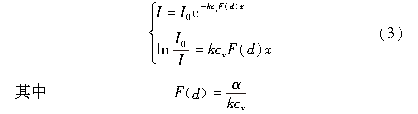

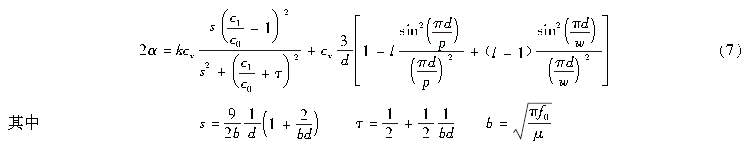
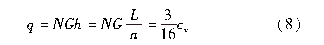
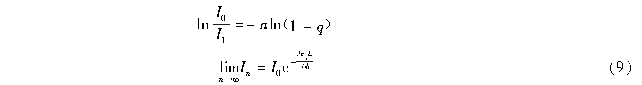

 空气耦合式超声波无损检测技术的
06-08
空气耦合式超声波无损检测技术的
06-08
 超声波测距系统
04-15
超声波测距系统
04-15
 超声波声速测量新方法
06-05
超声波声速测量新方法
06-05
 超声波探伤实验
09-24
超声波探伤实验
09-24
 超声波测距仪研究
06-03
超声波测距仪研究
06-03
 超声波在悬浮液中的衰减
06-09
超声波在悬浮液中的衰减
06-09
