1.简介
铅基压电陶瓷,如锆钛酸铅(PZT)由于其优良的压电性能,广泛应用于致动器、传感器和传感器中[1,2]。然而,在制造、使用和处置此类装置时会产生有害物质。因此,人们认识到需要开发无害环境的无铅材料[3–5]。无铅压电材料可以描述为钙钛矿,如BaTiO3、KNbO3和NaTaO3,或非钙钛矿,例如铋层结构铁电(BLSFs)和钨青铜型铁电[6]。钛酸铋(Bi4Ti3O12;BIT)是最有趣的BLSF化合物之一[7]。它显示出居里温度高(675◦C) 介电常数低(127-154),高机械质量因数(5900),低老化率。因此,它有可能用于航空、航空和汽车工业中使用的压电器件,并且应在高温下工作,如先前的研究所示。例如,Daichi等人[8]制造了具有700热耐久性的LiNbO3/位超声换能器◦C、 而谢等[9]通过W/Nb取代提高了比特基Aurivilius陶瓷的压电性能和温度稳定性。Xu等人[10]利用BIT和Ceramabind830和Megriche等人[11]制备了高达500个稳定性良好的钻头陶瓷,用于高温应用◦C.
一般来说,钻头的弹性、介电和压电常数在设计压电器件之前应确定。如果已知这些常数,研究人员可以进行数值模拟,以评估压电器件的性能。北岛
等人[12]使用电共振法测定了位单晶的弹性柔顺常数(sE11、sE22、sE33和sE66)、压电常数(d11、d12、d13和d26)和耦合因子(k11、k12、k13和k26)。此外,舒尔曼等人[13]研究了钻头的微观结构、导电性和压电性能,Kozielski等人[14]研究了低温燃烧合成的钻头陶瓷的介电弛豫。Nagata等人研究了晶粒取向钒钻头陶瓷的高温压电常数d33和耦合因子k33,以及压电常数k33和弹性柔顺常数sE33对Nd和V共取代位ce ramics的温度依赖[16]。Villegas等人[17]从共振和反共振频率出发,确定了W掺杂钻头压电参数kp和d31的温度依赖性。
然而,由于几个原因,钻头陶瓷和单晶的全矩阵常数,包括弹性常数、压电常数和介电常数,都没有得到表征。首先,生长的位元单晶总是以非常薄的血小板的形式存在,这使得我们不需要描述它们的全矩阵常数[18]。第二,位单晶具有单斜对称[7,19–21]。其中,有13个独立的弹性常数,10个独立的压电常数,4个独立的介电常数。对如此大量材料常数的表征是非常必要的。此外,钻头陶瓷具有低电阻率和大的矫顽场,阻碍了极化过程。因此,掺杂一种或多种元素常常被用来增强位元基材料的压电和铁电性能。例如,掺杂有给体阳离子的位陶瓷,例如Nb(V)和W(VI),使导电性降低至少一个数量级[7,22,23]。然而,掺杂形成了一种更复杂的结构;因此,在制备过程中保持钻头陶瓷的均匀性是一个挑战。更具体地说,确保制备的大钻头样品仍然具有良好的均匀性是非常必要的。例如,富士陶瓷公司(Fujicera)的极化钻头产品厚度只有2mm。
超声脉冲回波(UPE)法和IEEE阻抗共振法通常用于表征压电材料的完整矩阵常数[24]。UPE方法可以用来确定各向异性样品的某些弹性常数而不是全部弹性常数。阻抗谐振法在表征过程中需要多个几何尺寸大不相同的样品。位样本的小尺寸限制了该方法在其表征中的应用。k15谐振器可以作为一个例子来说明这个问题。k15谐振器沿x、y和z方向的尺寸分别为t、w和l,其中z是偏振方向。理论上,为了保证表征的准确性,l和w应该比t大得多。在实际测量中,通常要求l/t和w/t都超过10。如果l为2 mm,则t应小于0.2 mm。当这样一个薄的样品被连接到阻抗分析仪的打印机夹持时,可能会出现较大的测量误差。此外,使用阻抗共振法表征的完整矩阵常数可能不一致,因为在表征中使用了多个样品[25–27]。
在本研究中,共振超声光谱(RUS)技术被用来测定钻头样品的弹性常数。RUS适合描述钻头,原因有以下两个。首先,它可以表征非常小尺寸(<1 mm3)样品的材料常数[28–30]。第二,该技术可用于表征具有高机械品质因数(QM)的样品,而BIT的机械品质因数约为5900。早在1990年,Ohno[31]首次利用RUS检索压电材料的弹性常数。Ogi和他的同事[32–34]描述了铌酸锂的完整基体常数,α-石英和GaN,它们都有很高的QM。在另一项研究中,Tang等人[27]通过RUS测定了PZT-4的全基体常数的温度依赖性,而Chen等人[35]利用RUS表征了单畴0.72 Pb(Mg1/3Nb2/3)O3–0.28PbTiO3单晶的弹性和压电常数。最后,Xiang等人[36]利用RUS对单畴Pb(Zn1/3Nb2/3)O3–6.5%PbTiO3单晶的弹性和压电性能进行了表征。
UPE和RUS的结合仅使用一个压电样品来表征钻头陶瓷样品的所有弹性常数。用阻抗分析仪直接测量同一样品的介电常数。压电应力常数e31和e33可用不同材料常数之间的关系式计算。根据RUS反演结果,假设e15的值约为零。因此,从同一样品中测定所有常数,以确保结果的一致性。
2.方法
2.1. 共振超声光谱学原理
RUS包含两个问题:正问题和逆问题。RUS正演问题使用瑞利-里兹方法根据样品的材料常数和几何尺寸计算共振频率。RUS反问题使用最小二乘法根据测量的样品共振频率反演材料常数。
其中,CL3和CH3分别是沿z轴方向的低频和高频电容;l、w和t分别是沿x、y和z轴方向的样本大小。表1列出了位样品的相对介电常数。
2.2.3. 某些弹性常数的测量
用UPE法测定了钻头试样的弹性常数。用10mhz纵波换能器(Olympus,CN10R-5)和5mhz横波换能器(Olympus,V156-RM)分别发射和接收纵波和横波。传感器由30 MHz脉冲发生器/接收器(Goworld Co.,Ltd.)激发,回波之间的光照时间由方法确定。使用cE12=cE11-2 cE66计算的cE12值为4.09× 1010
牛/平方米。注意,UPE确定的cE11、cE12、cE44的值可以用作RUS反演中的初始值。
2.2.4. 共振超声光谱的测量
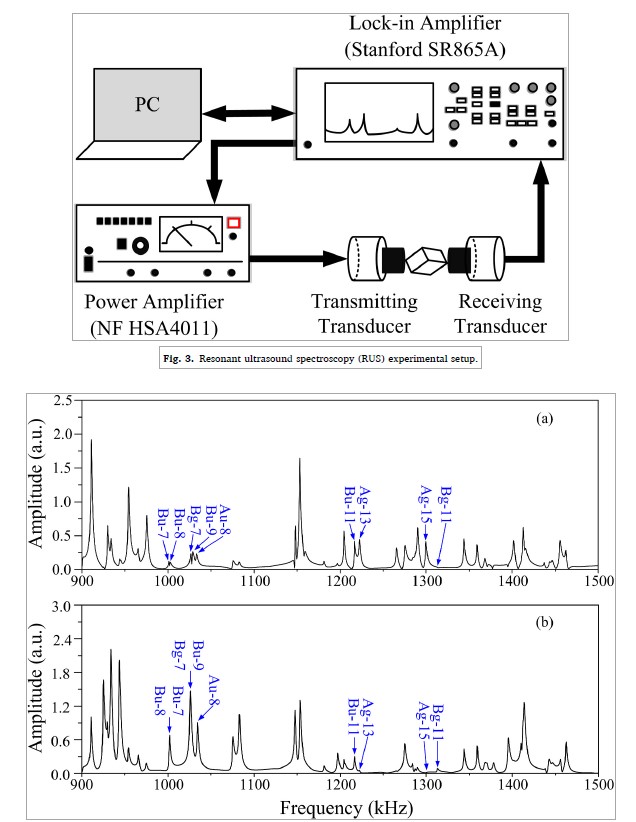
图3显示了RUS实验装置,包括传输和接收传感器、NF HSA4011功率放大器、斯坦福SR865A锁定放大器和个人计算机(PC)。样品固定在发射和接收传感器之间,仅在相对的角落接触。锁定放大器产生扫频信号,扫频信号是功率放大器的输入,因此被放大。发射换能器由放大信号驱动。因此,样品的振动被激发。接收传感器感测到振动,并将其转换为电信号输入锁定放大器。处理后,样品的共振光谱从锁定放大器输出并显示在PC上。
3.结果与讨论
3.1. RUS结果
在RUS中,样品位置显著影响测量的共振超声光谱。在被测频谱中丢失的一些模式可能发生在另一个位置。为了进行精确的模式识别,通过改变样品位置测量了300至2000 kHz的多组光谱。图4显示了钻头样品在900至1500 kHz范围内的两组超声共振光谱。根据变形对称性,矩形平行六面体钻头陶瓷样品有四个振动组,分别用Ag、Bg、Au和Bu表示[31]。模式Bu-7和Bu-8以及Bg-7和Bu-9重叠。它们无法从图4(b)中识别;然而,它们可以从图4(a)中识别出来。模式Ag-13和Ag-15可以从图4(a)中精确识别,但从图4(b)中很难识别。同时,模式Bg-11可以从图4(b)而不是图4(a)中识别出来。利用上述两个方程,从测量的困难中确定了75个共振模式,以精确确定钻头样品的e15值。然而,RUS分析的反演结果可以提供e15的近似范围。表4显示e15的值非常小。因此,我们假设e15的值大约为零。
3.4. 全矩阵常数
钻头陶瓷的其他材料常数可以通过RUS使用75个共振模式(表4)、固定介电常数(表1)和压电应力常数(第3.3节)确定的恒定电场的弹性刚度常数来计算。表5显示了钻头陶瓷样品的全部基体材料常数,包括恒定电场cijD下的弹性刚度常数;弹性刚度
恒电位移常数;弹性柔度控制-
恒定电场sEij;恒位移弹性柔度常数sijD;压电电压常数;压电刚度常数;压电应变常数dij;自由和钳位介质隔离率βTij和β分别为Sij;机电耦合常数kij。
3.5. 结果验证
表3中的fcal值是用表5所示的弹性常数、压电常数和介电常数计算的共振频率。测得的共振频率与计算的共振频率之间的相对误差如表3所示。大多数误差小于0.3%,这表明本文所确定的结果是可靠的。图7显示了500至2000 kHz的电阻抗曲线,其中红色虚线是使用通惠2838H阻抗分析仪测量的,蓝色虚线是使用ABAQUS(Dassault Syst`emes Simulia Corp.,Providence,RI)计算的。在模拟过程中,通过RUS使用75种模式确定弹性常数,如表4所示。表1列出了固定介电常数,第3.3节给出了压电常数。应使用复材料常数来模拟精确的电阻抗。有限元模拟中仅使用了真实的弹性、压电和介电常数。因此,测量阻抗和模拟阻抗的振幅通常不一致。
然而,共振和反共振频率是由实际材料常数决定的。图6显示,大多数测量和模拟的共振和反共振频率符合得很好。这一发现验证了本研究中确定的钻头材料常数的可靠性。
4.结论
IEEE阻抗共振法需要多个尺寸完全不同的压电样品来确定它们的全矩阵常数。然而,制造大型、高质量的极化钻头陶瓷非常困难。因此,钻头陶瓷的完整基体常数尚未公布。为了解决这一问题,本研究引入RUS来表征钻头陶瓷。RUS适用于高QM小样品的材料常数测定。通过UPE和RUS仅使用一个小样品测定钻头陶瓷样品cE11、cE12、cE13、cE33和cE44在恒定电场下的五个独立弹性常数。钳位介电常数εS11和ε钻头样品的S33由阻抗分析仪测得的高频电容确定。用UPE法测定了cD33的弹性常数。利用不同材料常数之间的关系式,计算了钻头的压电应力常数e31和e33。根据RUS反演结果,假设e15的值约为零。为了验证测定结果的可靠性,用这些结果计算的电阻抗谱与用阻抗分析仪直接测量的电阻抗谱进行了比较。
本文的研究结果将有助于钻头陶瓷压电元件的设计。此外,由于RUS能够测定弹性常数的温度依赖性,本研究提供的测定程序为测定钻头陶瓷全基体常数的温度依赖性铺平了道路。