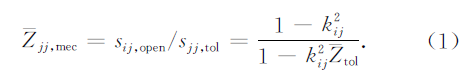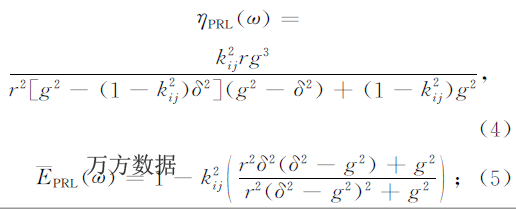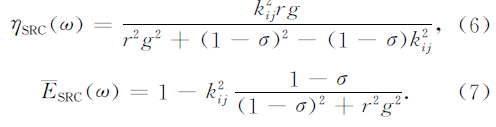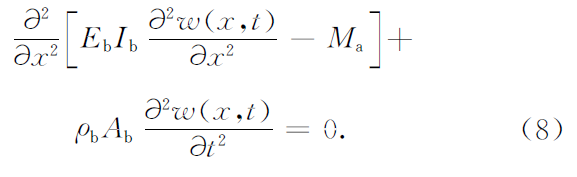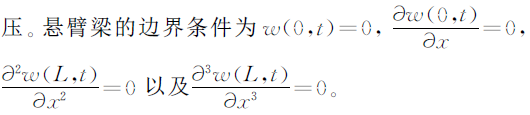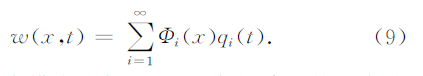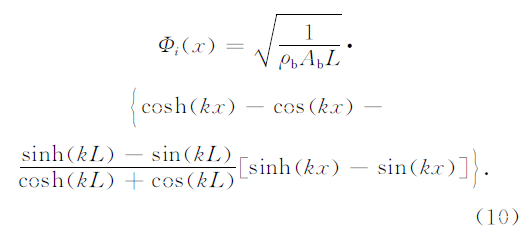压电陶瓷作为一种新兴的功能陶瓷材料在很多技术领域均得到了广泛应用,其中也包括在结构振动控制领域的应用G由于具有将机械能与电能相互转化的能力,因此可以作为传感器或作动器嵌入到系统之中,用于结构振动的主动控制。当压电陶瓷材料与外界电路组成闭合回路时,由于机电耦合作用,会表现出一定的阻尼特性,这种特性可以用于结构的被动控制。
1979年,Forward首先提出了将压电陶瓷与电路元件并联,用于振动控制的可能性,其后Hagood和von Flotow对压电陶瓷与外界电路的机电耦合特性进行了理论建模,并研究了压电陶瓷分别与纯电阻电路和串联电阻电感电路并联时对悬臂梁振动的影响,实验结果与理论结果吻合良好,从而系统地证明了压电陶瓷与外界电路并联用于振动控制的可行性。此后,许多研究人员都开始投入到了这一领域的研究。
为了更好地将并联压电陶瓷的阻尼特性应用于振动控制,本文在文【2】研究工作的基础之上,对压电陶瓷与电阻电感并联和电阻电容串连电路并联耦合的阻尼特性建立理论模型,并基于悬臂梁系统对理论模型进行了验证,为压电陶瓷在被动控制领域的应用提供了理论基础。
压电陶瓷材料具有将机械能转化为电能的性质。如图1所示,当压电陶瓷受外力作用时,表面会产生电荷。若压电陶瓷处于开路状态,电荷会聚集在压电陶瓷的表面。当压电陶瓷与外界电路形成一个闭合回路时,一部分电荷会被电路中的阻抗以热能的形式消耗掉,也就是说一部分机械能被以热能的形式释放掉。这就是压电陶瓷与外界电路并联用于振动被动控制的机理。
1.2理论模型
从电学角度来看,压电陶瓷可以简化为一个电压源和一个电容的串联模型。图2为压电陶瓷与外界电路并联的等效电学模型。
并联压电陶瓷的量纲1机械阻抗为
式中:kij为压电陶瓷材料的机电耦合系数,Ztol为量纲1电学阻抗,由下式决定:
式Ztol和Zopen分别为外界电路为闭路和开路时系统的电学阻抗。
机械阻抗Zjj,mec等效于压电材料的力学刚度,因此,并联压电陶瓷的阻尼特性,即能量耗散因子ŋ和刚度比E可分别定义:
式中Im{Zmec(s)}和Re{Zmec(s)}分别为量纲’机械阻抗的虚部和实部,s为Laplace因子。
由式(1)~(3)可以得到外界电路分别为电阻电感并联和电阻负电容串联电路时,压电陶瓷的材料阻尼特性模型:
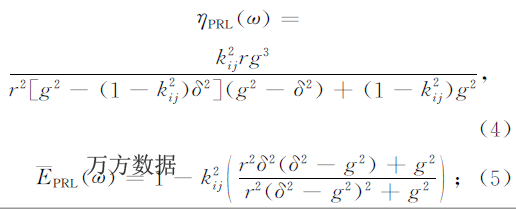
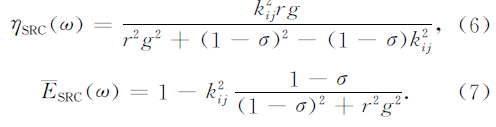

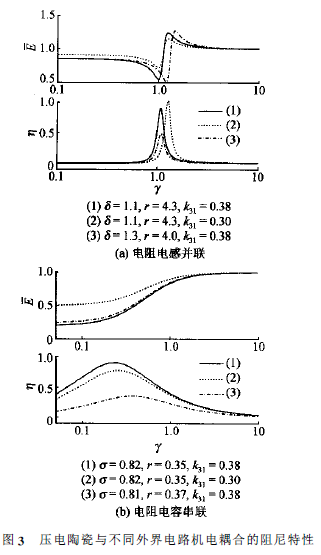
由上面的模型可以看出,压电陶瓷的阻尼特性与压电陶瓷的机电耦合系数,工作频率和谐振因子均有关系。图3给出了压电陶瓷在不同外界并联电路情况下的阻尼特性曲线,以及各个参数对阻尼特性的影响。
由图3可以看出,并联压电陶瓷的阻尼特性和很多因素有关系,如压电陶瓷本身的特性,外界电路的类型,以及具体的电路参数。随着这些因素的变化,压电陶瓷表现出不同的阻尼特性。
2 基于悬臂梁系统的仿真研究
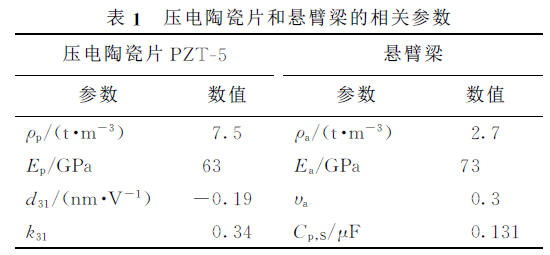
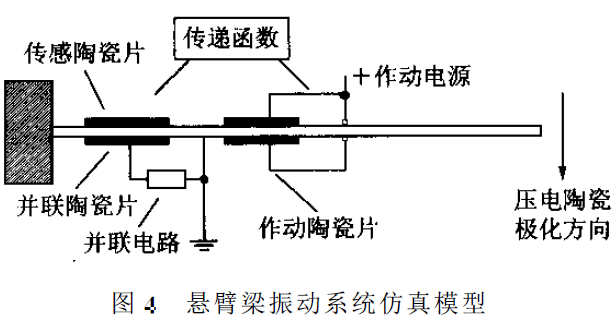
为了验证电路类型及相关参数的变化对并联压电陶瓷阻尼特性的影响,设计了一套基于悬臂梁的仿真系统,如图4所示,,4片(2对)PZT-5压电陶瓷片粘贴于悬臂梁的表面,梁表面接地,压电陶瓷片极化方向如图所示。4片压电陶瓷片中,2片为作动器,作为悬臂梁振动的驱动源;一片作为传感器,通过测得的电压值来反应悬臂梁上相应位置的振动强弱;另外一片与外界电路并联,第一对压电陶瓷片的尺寸为60mm*26.4mm*0.25mm,第二对为50mm*26.4mm*0.25mm。2对陶瓷片左端距悬臂梁固定端的距离分别为18mm和100mm。系统的输入与输出,即作动器的输入电压与传感器的输出电压之间存在一定的传递函数关系。通过比较外界并联电路为开路和闭路情况下的传递函数,可以确定并联压电陶瓷对系统振动的影响。
首先建立传递函数模型。采用压电陶瓷片驱动的悬臂梁的一维Bernoulli-Euler方程如下:
式中Eb 、Ib、Ab、ρb分别代表悬臂梁的弹性模量、转动惯量、截面积和密度。Ma=KaVa(χ,t)为压电陶瓷作动器作用于悬臂梁中性层的力矩,Ka为与作动器性能有关的常数,Va为施加于作动器上的电
悬臂梁上任意一点的位移函数可以表示为
式中:qi(t)为模态坐标,Φi(χ)为悬臂梁的正交化模态振型函数,可以由下式确定:
采用文【8】介绍的方法,可得到开路与闭路时输入电压与输出电压之间的传递函数分别为:
根据以上模型,对电阻、串联电阻电感、并联电阻电感和并联电阻负电容4种情况下压电陶瓷对悬臂梁系统振动的影响进行了仿真研究。负电容通过负阻抗转换电路来实现。仿真用到的悬臂梁和压电陶瓷的相关参数见表1,仿真只涉及到了悬臂梁第一阶模态,考虑了电阻的变化对压电陶瓷阻尼特性的影响。仿真结果如图5所示。
由图5可以看出,不同的并联电路情况下,压电陶瓷片对悬臂梁系统振动的影响很大。对于同一种电路,阻尼效应随着电阻值的改变而改变,且从变化趋势来看存在着一个最优值。这与前一部分的理论模型完全相符。通过比较可以看出,与电阻并联时产生的阻尼效应最小,而与电阻负电容串联电路并联时产生的阻尼效应最强。对于两种电阻电感并联电路,压电陶瓷片对系统的影响比较相似,但阻尼性能随电阻变化的敏感度却相差较大。而且,当串联电阻电感电路的电阻值由大变小,而并联电阻电感电路的电阻值由小变大时,它们对悬臂梁系统性能影响的趋势则相同。考虑到并联压电陶瓷片本身的阻尼特性和其对系统性能的影响,综合比较的结果是压电陶瓷片与电阻负电容串联电路耦合的性能最好,不仅具有最大的阻尼,而且有较大的带宽。
3 结论
本文对压电陶瓷片与2种不同的外界电路并联情况下的阻尼特性进行了理论建模,并仿真研究了压电陶瓷与4种不同外界电路并联条件下对悬臂梁系统振动性能的影响。验证了压电陶瓷片与不同的外界电路耦合时具有不同的阻尼特性。通过比较得出,压电陶瓷片与电阻负电容串联电路并联时,具有较大的带宽#并能产生最大的阻尼。这提供了一种用于结构振动抑制的被动控制方法。
作者:张付兴 阎绍泽
(清华大学 精密仪器与机械学系,北京100084)