3. 2. 3 ���������еĴ�����������
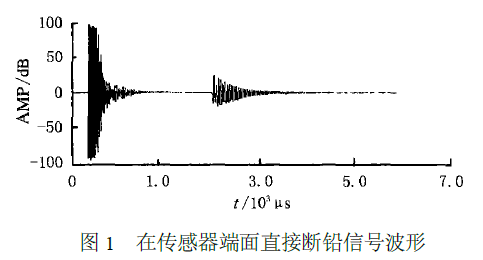
��Ǧ�������źŴ���ǰ�����뾭�����˴�����õ����������źŲ�������2 ,3. ͨ����3 , �ɵõ�������ֱ�����״��źŷ�ֵ�Ĺ�ϵ. ��������������ʱ����ֱ�����Ӷ�������,û�����Ա仯���ɡ�
3. 2. 4 ���������еĴ����ٶ�
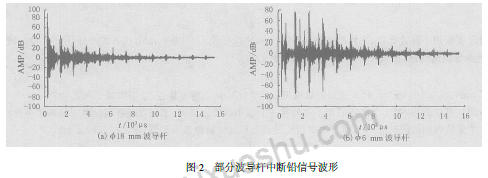
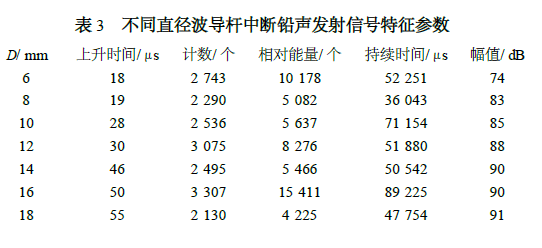
��ͼ2 ��֪, �������õIJ���ʱ����, �����������ϵõ��IJ�������ʮ�����źŷ���. ͨ��ʱ�������֪,���ڲ�����ʱ�����. �����ƶϵ�2 �������ǵ�1 ������ķ��䲨,��3 �������ǵ�2 ������ķ��䲨,�Դ�����. �ɴ˸������ڲ�����ʱ��Δt �������˳���L ,�����ģ���ź��ڲ������еĴ����ٶ�v Ϊ:
����ʵ����7 �ֲ�����,ƽ��ʱ��Δt = 1 184μs ,ƽ���˳�ŠL = 3 000 mm ,����ʽ(9) ��õ�v = 5 068m/ s. ��Ϊ�ݲ��IJ���,�ɼ�����,�ݲ��ٶ�vp Ϊ
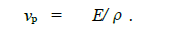 (10)
(10)
��ρ= 7. 80 ×103 kg/ m3 ����ʽ(10) ��ɵ�vp = 5 064 m/ s ,��v �ӽ�,֤��ʵ������ȷ
��ͼ2 ���Կ���,��1 ��������治Զ����һ����С��ֵ�IJ���(����ֱ�������˲�����) ,��С�������1 ����������ʱ��ΪΔt′,�����ڳ���7 �ֲ����������ֵ�������,��˺Შ����vl Ϊ
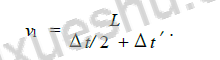 (11)
(11)
��ʵ��ŠL = 3 000 mm ,Δt = 1 184μs ,ƽ������ʱ��Δt′= 368μs ,����ʽ(11) ,�õ�vl = 3 125 m/ s. ģ���������ź��ڲ����˵�2 ������䴫��ʱ,�������䡢�����,�������ֲ���ת��. ��ʵ�ʼ����,Ӧ���Ƕ��ֲ��ʹ��ڻ���ת���Լ����������һЩ���Ӱ��.
��ͼ2 ��ͼ3 ��֪,�������źž��������˺�,�䲨�η�����Ӧ�仯,���Կ���ÿ��ֱ���IJ����˲���ͼ�϶���10 ��η���,˵���������źž��ɲ����˴������˥���dz�С. ͨ����������,Ҳ֤������һ��. ���ò����˽��и�������Ϊ����.
��ͼ3 ��֪,�ڲ�ֱͬ�����������źŵķ��ȱ仯����, Φ10 , Φ8 ,Φ6 mm Сֱ���˲���ͼ�ںεķ����з�ֵ�������½�. �������źž����η����,���Ⱦ�������������,�������ݲ��ͺᲨ���ٲ��������2 �η����źŵ�������.
 ��1��
��1��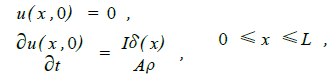 ��2��
��2��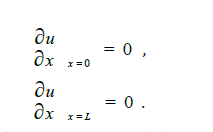 ��3��
��3�� ��5��
��5��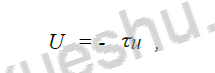 (6)
(6)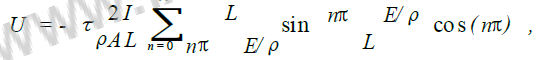 (7)
(7)


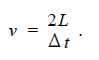 (9)
(9)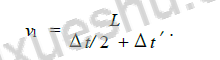 (11)
(11)